Name: Michelle Loomis

Childhood/Early Childhood Department

Lesson Plan

Date of Lesson Oct 17^th 2008 Time _____ Length of lesson 30-40 minutes

Curriculum Area Mathematics Content Area: Multiplication

Title of Lesson Multi-Digit Multiplication

Age/Grade level 3^rd/4^th Grade

Differentiation of activity is to be provided throughout the lesson plan to ensure that children’s individual learning needs are met.

1. Learning Objectives

Students will be able to multiply one digit numbers by multi-digit numbers using a partial-products algorithm.

2. Assessment

(a) Learning outcomes of previous lesson related to this topic:

Students will need to understand their multiplication facts. They will also need to understand the purpose of place value and its significance in solving a multiplication problem.

(b) Focus of assessment in this lesson:

Students will be able to explain how to multiply two digit numbers by one digit numbers using a partial-products algorithm. They will point out each step in the process and be able to use that method to multiply larger numbers.

(c) Method of assessment used in this lesson:

Throughout the lesson I will be assessing how well the students comprehend the new material being taught. I will do this by asking questions, walking around and observing, and working one-on-one with students who are having difficulty. A homework assignment will also be sent home for the students to practice their new knowledge. This assignment will be brought back the next day, and I will grade it and determine what students need extra help and what students understand the new method.

(d) Differentiation:

Time will be provided to help the students who do not understand the new topic. This time will be during recess, after school, or whenever there is time throughout the day. If not enough time is found then I will set aside a day to review in smaller groups where the students who need more guidance will be able to review. During time that is found a new way of teaching this method will be brought up. The use of counting blocks, re-explaining the topic, and/or reviewing their prior knowledge on multiplication and place value, will be used.

3. New York State Learning Standards

3.N.4 – Understand the place value structure of the base ten number system
4.N.18 – Use a variety of strategies to multiply two-dgit numbers by one-digit numbers (with and without regrouping)

4. Materials

· Number Cards

· Times Table

· Homework Sheet

· White boards and markers

5. Lesson Process

(a) Introduction (5 min.)

Students in the previous lesson would have used building blocks and graphs as arrays to see what multiplication really means. An array will be shown on the board to engage the students. The students will be told that they will be able to figure out how many dots are on to board without counting each single dot, or adding each line.

…………………..

The students will then be told that first they need to review their multiplication tables. Students will be asked to take out their multiplication tables and work with a partner to quiz each other. Partners will be picked by pairing up students who are sitting around each other. After three minutes the students will be asked if they remember learning about place value. Two digit place value will be reviewed on the board. Students will need to understand where the ones place is and the tens place. Students will also be reminded of the meaning of a number. The example, 46 will be used. Students will have to understand that 46 actually means 40 + 6. The teacher will then explain that the students are going to learn today how to multiply bigger numbers, then just 5 x 6 and 8 x 4, and that they need to use place value to figure out the answer.

(b) Learning procedures relating to objectives (30 min.):

Each student will be given a white board for this activity. Their attention will then be turned to the main board and the first example will be given:

A fourth grade class had 46 boxes of crayons. Each box had eight crayons in it. How many crayons did the class have in total?

The students will be instructed to write down how they think they should answer this question on their white board. Students will be asked if they know what the first step to answering this question is. If a student does, they will be asked to explain how they would do the problem. Then the teacher will go through the steps as a class. “The first step is to multiply the tens place value by the bottom number (40 x 8 = 320). Then you would multiply the ones place value by that same bottom number (6 x 8 = 48).” Then the students will be asked to add the two numbers and whatever the answer to their addition problem is, is the answer to their beginning multiplication problem.

320

+ 48

368

Possible questions at this point:

· How do I multiply 40 by eight?

o Answer – uses addition to solve the problem with the student. 40 + 40 = 80 + 40 and so on. Then have the student rewrite the problem as 8 x 4 x 10. By doing this the student will get 32 x 10 = 320. This will show the student the purpose of the zero.

· I only got 80, why?

o Answer – If a student got eighty because they forgot the zero when multiplying 8 times the tens place (40). They instead forgot that the zero needs to be there and just multiplied 8x4. Therefore, it needs to be explained that they forgot that the four is in the tens place, so the zero has to be a place holder. Show this by writing forty out for them, adding six: 40 + 6 = 46.

The lesson will continue by doing another example as a whole group:

120

The students will then be able to try a problem on their own:

420

+12

432

Students will be asked to do this problem on their own on the white board. After most students are finished, the class will work together on coming up with an answer to the problem. I will monitor the students by walking around the class and helping out students who are confused.

Another practice problem will be given, following the same format as before:

720

+32

752

The next part of the lesson will have the students working in groups of two or three. Each group will be given two piles of cards, and will be instructed not to mix up the cards. One set of cards will have the tens place values on it, such as 10,20,30,40 etc…and the other will have the ones place values on them, such as 0,1,2,3,4,5,6. Students will also be given WORKSHEETS that have spots for them to place the cards in the correct place value. The object is for students to understand where to correctly place the cards, keeping in mind that the “zero” is being covered up in the tens place value.

For the first problem I will give them the problem on the board and the students will have to find the corresponding cards. This will help to show that they understand how this activity is going to work. I then will ask them to solve the problem using their pencils and not the cards.

4

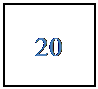Text Box: 20 x3

Text Box: 4

3

x

Text Box: 60,Text Box: 12

+

2 0

After that problem is solved the students will be instructed to develop their own problems with their partners (or groups). The students will be told that they need to pick one number from the two digit pile and two numbers from the one digit pile. One group member will select the numbers first for the other to solve, and then the next member will select the numbers, and so on.. The students will do this for 5-7 minutes. During that time I will walk around to make sure the students understand the concept.

(c) Conclusion (2-3 min.)

I will then ask for a few volunteers to write problems on the board that they came up with, in their groups. I then will ask everyone to solve them on their white boards and ask for someone to volunteer the answer.

The lesson will come to an end by answering any remaining questions and concerns the class seems to have. I then will hand out their homework, and explain that they should try the last problem. I will then explain that tomorrow we will be talking about multiplying single digit numbers by triple digit numbers.

6. “If time”/ extensions

If a significant amount of time is left, then I will move the class onto multiplying 3 digit numbers by one digit. This lesson will be conducted the same way as the previous lesson. If only a few minutes are remaining then I will let the students begin their homework, allowing them the opportunity to ask questions if they are still confused.

7. References

“Everyday Math”. Unit 9 – Multiplication and division. 9-4 A Multiplication Algorithm.